Strategy
Price will allow users to jump into a shared concentrated strategy. But what is the point of a concentrated position?
- More liquidity means easier arbitrage and more precision for the oracle
- Efficiently compete for fees against external liquidity providers
We plan on opening this part of the protocol so that users can participate using any Uniswap V3 position manager like Revert, Arrakis, etc. For the alpha launch, we will have our own strategy.
The strategy will only accept WETH deposits. We don't concentrate on the other token as well, because the parameters for setting the strategy triggers are computed based on gas costs. This is doable with WETH, but not so much for extremely volatile assets. Notice the protocol is fully permissionless.
When do we deploy the liquidity?
The total available WETH will not be deployed as users lock WETH, but it will be batched instead. This reduces the risk of misplacing liquidity and minimizes gas costs for liquidity providers. Each batch will deploy half of the available WETH: notice this is asymptotical, meaning the LockManager never runs out of WETH to deploy in extreme IL situations.
The liquidity will be deployed once a minimum amount of WETH is reached. This minimum amount is such that the gas costs of deploying and collecting fees are much smaller than the generated fees. In this way, positions never go at a loss due to gas management.
To trigger the maintenance jobs, excluding manipulation correction, the contract will check that the gas costs represent a fixed percentage of the total accused fees. The strategy also has a maximum amount of WETH defined, which can be deployed in each batch. This restriction, even if suboptimal from a gas perspective, is also necessary to minimize liquidity misplacement risk. As we are running the jobs only when enough fees have accrued, the protocol will be self-sufficient.
We're not using a time trigger because, while unlikely due to arbitrage, it might trigger even with 0 or almost 0 trading volume, and the protocol would be at a loss.
Another option would be to trigger at the edge of the current position. The problem with this approach is that fee collections would be much harder and that we would stop the price discovery mechanism by deploying liquidity in bad prices. Also, it might be invisible to large trades and it can be manipulated.
Dynamics
Price of WETH increases relative to the other token
A part of concentrated liquidity gets swapped for the other token. When the fee threshold is met, a new position gets deployed.
If we assume that WETH is token0 in the pool, then it can be pictured as being to the right of the current price (limit orders of WETH above the current price).
Position0 was deployed when price was \(P0\). Then, the price increased and position0 was partially turned into TOKEN. When the spot price reached \(P1\), the generated fees and the available WETH allowed for the deployment of position1.
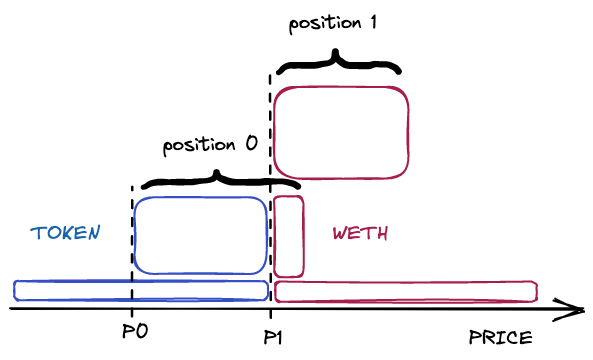
Concentrated positions of TOKEN that became single-sided positions can be re-positioned close to the current price. We will not do it in the alpha version, since doing so assumes and closes IL, which would not happen with WETH.
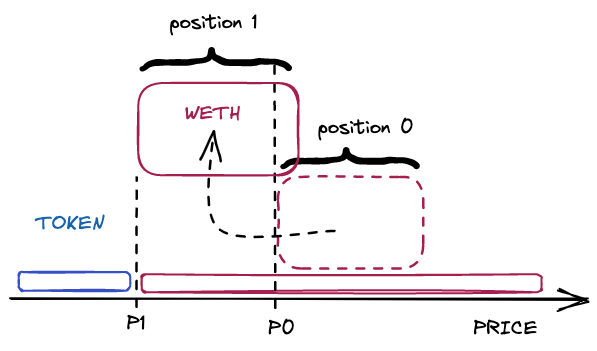
Price of WETH decreases relative to the other token
When the price of WETH decreases relative to the other token, a new WETH position is deployed when generated fees reach the threshold. If a WETH position is too far from the current price, the position is burnt and the WETH goes back to the LockManager, ready to be deployed.
The shape of the positions
We determined the width of the positions with a set of restrictions
- The more assets to mint, the less percentage of risk. Big capital looks for safety and prefers wider positions, and small capital risks more.
- Even if we are not running the job until having enough fees, each position should justify its minting cost without a doubt.
- We want the position to be used as much as possible without resigning too much liquidity. Remember concentration effect on liquidity can be huge.
- As a heuristic approach, positions will tend to the safer end in this release. In v2 we plan to introduce riskier takes, e.g. allowing several LockManager contracts to live in the same pool.
Note that we think of narrow positions as risky because in the worst-case scenario with high volatility, thin positions have the worst performance, generating zero fees.
A way to achieve these goals is to mint a fixed amount of liquidity and make the number of assets determine the width. The challenge here is determining the right amount of liquidity. Note that how we measure liquidity is not objective but changes from pool to pool. To define this liquidity, we can define a minimum amount of WETH and a min-width for it. This will be chosen such that positions are self-sustainable, and with the assumption that the position is used most of the time. This can be broadly estimated using some quantitative finance and historical volatility. Finally, we will assign an overestimated volatility that will determine this minimum width.
We will take a "linear strategy" as a function of assets that is simple to code. We will fix the values \(r_{min}\) and \(r_{max}\), \(Amount_{min}\) and \(Amount_{max}\), where \(r\) is defined as
\(r=\sqrt{\frac{p_{upper}}{p_{lower}}}\)
with \(p_{upper}\) and \(p_{lower}\) the upper and lower bounds of the position. Then, create a linear function such that
\(\sqrt{p_{upper}} = a*Amount+b\)
\(a\) and \(b\) can be found by simply making the line fit through the points \((\sqrt{p_{upper_min}},Amount_{min})\) and \((\sqrt{p_{upper_max}},Amount_{max})\)
\(\sqrt{p_u} = r_{min}\sqrt{P}\) and for amountMax \(\sqrt{p_u} =r_{max}\sqrt{P}\)
A line going through two given points is given by
\(\frac{y-y_2}{y_1-y_2}=\frac{x-x_2}{x_1-x_2}\)
\(\sqrt{p_u}=\)
\(\sqrt{P}\left[\left(\frac{r_{max}-r_{min}}{Amount_{max}-Amount_{min}}\right)(Amount-Amount_{min})+r_{min}\right] = \frac{\sqrt{p_{upper_max}}-\sqrt{p_{upper_min}}}{(Amount_{max}-Amount_{min})}(Amount-Amount_{min})+\sqrt{p_{upper_min}}\)
The same can be applied to the case of WETH being token1
\(\sqrt{p_{lower}} = a*Amount+b\)
\(a\) and \(b\) can be found by simply making the line fit through the points \((\sqrt{p_{lower_max}},Amount_{min})\) and \((\sqrt{p_{lower_min}},Amount_{max})\)
\(\sqrt{p_l}= \frac{\sqrt{p_{lower_min}}-\sqrt{p_{lower_max}}}{(Amount_{max}-Amount_{min})}(Amount-Amount_{min})+\sqrt{p_{lower_max}}\)